ALGORITMOS Y PSEUDOCÓDIGO EN PSEINT

¿QUE ES PSEINT?

PseInt (Pseudo Intérprete) es un Entorno de Desarrollo Integrado (IDE, por sus siglas en inglés) para PseudoCódigo, un lenguaje de programación imperativa simple y en castellano.

Es decir, PseInt es un editor e intérprete de programas escritos en PseudoCódigo. Su interfaz gráfica permite crear, almacenar, ejecutar y corregir fácilmente programas en PseudoCódigo.

La sencillez del lenguaje PseudoCódigo lo hacen ideal para la enseñanza de la programación. Permite escribir programas con instrucciones condicionales (Si-Entonces-Sino, Según) y ciclos (Mientras, Hasta Que, Para), y también usar valores numéricos (números decimales), lógicos, caracteres y arreglos. También provee funciones de entrada/salida y algunas funciones matemáticas.

Vídeo 

¿QUE ES UN PSEUDOCODIGO EN PSEINT?

El pseudocódigo es un lenguaje de especificación (descripción) de algoritmos. El uso de tal lenguaje hace el paso de codificación final (traducción al 4 lenguaje de programación) relativamente fácil, por lo que este es considerado un primer borrador de la solución del programa.

La palabra pseudocódigo formada por el prefijo “pseudo“, que según el diccionario de la RAE (Real Academia Española) significa “falso“, de ahí parte para que también sea conocido como “falso lenguaje”.

Dentro de la programación se basa en un lenguaje de programación real, donde se permite expresar las instrucciones en un lenguaje común (ejemplo: español, inglés u otro idioma) para facilitar la escritura y lectura, debido a que está en lenguaje común si requiere una modificación es fácil hacerla. La escritura sólo puede ser comprendida por el ser humano y no por la máquina, por ende, tampoco puede ejecutarla. La finalidad de un pseudocódigo es representar la solución a un algoritmo (problema) de la forma más detallada posible, utilizando acciones sucesivas. Según Analía Lanzillotta: “Considerado como un lenguaje falso el pseudocódigo, que es un lenguaje intermedio entre nuestro lenguaje y el de programación, debido a que quien lo utiliza se guía por una serie de normas, pero sin llegar a usar una estructura tan rígida como la del lenguaje de programación”.Liga

En otras palabras, el pseudocódigo es un lenguaje simplificado entre el programador y la máquina, hecho por el programador en su propio idioma, para describir un algoritmo y  poder comprender mejor la estructura de dicho programa, donde el lenguaje simplificado no puede ser compilado, ejecutado ni corrido por la máquina. Siendo una herramienta que se encuentra previa al lenguaje formal de programación.

Vídeo.

TIPOS DE DATOS QUE UTILIZA PSEINT

Los datos son un conjunto de caracteres. Un carácter puede ser una letra, un numero, un símbolo.

Tipo Real: Una variable de tipo real admite datos numéricos, que pueden ser enteros y/o con punto decimal.

Tipo Entero: Es una especialización que sólo permite almacenar valores enteros; cualquier valor no entero que se lea o asigne en una variable de este tipo será truncado.

Tipo Cadena Es una secuencia ordenada (de longitud arbitraria, aunque finita) de elementos que pertenecen a un cierto lenguaje formal o alfabeto análogas a una fórmula o a una oración.

Tipo Carácter: Las variables de caracteres se usan para almacenar valores alfabéticos, en particular letras solas.

Tipo Lógico: Una variable de tipo LÓGICO sólo puede tomar los valores VERDADERO y FALSO, pero cuando se lee una variable ya definida como lógica, el usuario puede ingresar también las abreviaciones V y F, o 0 y 1.

DIAGRAMA DE FLUJO EN PSEINT

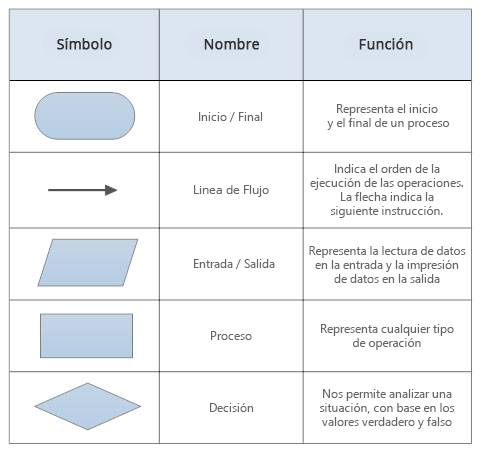
Un diagrama de flujo es un diagrama que utiliza símbolos (cajas) estándar y que tiene los pasos del algoritmo escritos en esas cajas unidas por flechas, denominadas líneas de flujo, que indican las secuencia que debe ejecutar el algoritmo

ESTRUCTURA SI - ENTONCES EN PSEINT

Al ejecutarse esta instrucción, se evalúa la condición y se ejecutan las instrucciones que correspondan: las instrucciones que le siguen al Entonces si la condición es verdadera, o las instrucciones que le siguen al Sino si la condición es falsa. La condición debe ser una expresión lógica, que al ser evaluada retorna Verdadero o Falso. 

La cláusula Entonces debe aparecer siempre, pero la cláusla Sino puede no estar. En ese caso, si la condición es falsa no se ejecuta ninguna instrucción y la ejecución del programa continúa con la instrucción siguiente.

 

ESTRUCTURA SEGÚN EN PSEINT

Es frecuente tener que comprobar más de una condición a la vez, o bien varias condiciones consecutivas. En concreto, un caso especialmente habitual es el de que una variable pueda un valor de entre varios. Por ejemplo, en el sistema de notas escolares español clásico, ciertas notas numéricas tienen "nombres" asociados: un 5 es un aprobado, un 9 y un 10 son sobresaliente, etc. Si queremos hacer un programa que convierta de la nota numérica a su equivalente escrito, podríamos emplear varias órdenes IF, una tras la otra. Pero en muchos lenguajes de programación (y por tanto, también en muchas variantes de pseudocódigo) existe una alternativa más compacta y más legible: la orden "SEGUN". Esta órden permite hacer unas cosas u otras según el valor que tome una variable. Su uso sería así:

El bloque "De Otro Modo" es opcional: si detallamos todos los valores posibles, no sería necesario utilizarlo.

El número de valores que podemos probar es indefinido: no tiene por qué ser 3, sino que pueden ser menos casos o muchos más.

Según la variante de pseudocódigo (o el lenguaje de programación) que empleemos, puede haber restricciones en el tipo de datos que es aceptable. Por ejemplo, en el caso de PseInt, la variable tiene que tener un valor numérico, no puede ser un texto.

Así, si en PseInt hacemos clic en el icono del panel derecho que representa la condición SEGUN, aparece un esqueleto de programa casi completo, para que hagamos los cambios que nos interesen:

Referencias Bibliográficas 

• Peter Norton, Introducción a la Computación,  Ed. Mc Graw-Hill.
• Luis Joyanes Aguilar, Fundamentos de programación. algoritmos y estructuras de datos, Ed. Mc Graw-Hill.
• Mario C. Ginzburg, Introducción General a la Informática, Periféricos y Redes Locales, Biblioteca Técnica Argentina.
• Armando E. de Giusti, Algoritmos, Datos y Programas, . Ed., Prentice Hall.
• Herbert Schildt, C Manual de Referencia, 4ta. Ed., Mc Graw-Hill, España, 2001.
• H.M. Deitel, J.P. Deitel, Cómo programar en C/C++, 2da. Ed., Prentice Hall, México, 1995.

Peter Norton, Introducción a la Computación,  Ed. Mc Graw-Hill.

Luis Joyanes Aguilar, Fundamentos de programación. algoritmos y estructuras de datos, Ed. Mc Graw-Hill.

Mario C. Ginzburg, Introducción General a la Informática, Periféricos y Redes Locales, Biblioteca Técnica Argentina.

Armando E. de Giusti, Algoritmos, Datos y Programas, . Ed., Prentice Hall.

Herbert Schildt, C Manual de Referencia, 4ta. Ed., Mc Graw-Hill, España, 2001.

H.M. Deitel, J.P. Deitel, Cómo programar en C/C++, 2da. Ed., Prentice Hall, México, 1995.

Peter Norton, Introducción a la Computación,  Ed. Mc Graw-Hill.

Luis Joyanes Aguilar, Fundamentos de programación. algoritmos y estructuras de datos, Ed. Mc Graw-Hill.

Mario C. Ginzburg, Introducción General a la Informática, Periféricos y Redes Locales, Biblioteca Técnica Argentina.

Armando E. de Giusti, Algoritmos, Datos y Programas, . Ed., Prentice Hall.

Herbert Schildt, C Manual de Referencia, 4ta. Ed., Mc Graw-Hill, España, 2001.

H.M. Deitel, J.P. Deitel, Cómo programar en C/C++, 2da. Ed., Prentice Hall, México, 1995.

Algoritmos Cuantitativos y Cualitativos

ALGORITMO: Es una serie de pasos organizados que describe el proceso que se debe seguir, para dar solución a un problema especifico.

Algoritmo Cuantitativo

Los algoritmos cuantitativos son aquellos en los que se utilizan cálculos numéricos para definir los pasos del proceso.

 Ejemplo: 

Este vídeo complementara tu información. 

Algoritmo Cualitativo

Son aquellos en los que se describen los pasos utilizando palabras.

Aquí un vídeo para reforzar información

Bibliografías. 

http://moodle2.unid.edu.mx/dts_cursos_mdl/lic/IC/EA/AM/06/Algoritmos.pdf

http://www.profmatiasgarcia.com.ar/uploads/tutoriales/Ej_resueltos_algoritmos.pdf

FUNDAMENTOS DE PROGRAMACIÓN

1.1 ¿En qué consiste la solución de problemas?

ANÁLISIS PREVIO DEL PROBLEMA

En esta etapa se debe definir y tener claro lo que el programa tiene que hacer junto con las tareas que debe realizar para llevar a cabo la solución, qué datos necesito para realizar la tareas, que formato deben tener los datos de entrada, de donde provienen los datos de entrada, como se obtienen esos datos, cómo interactúan los datos entre sí para obtener el resultado, muy importante tener claro cuál será el resultado que se desea obtener

CONFIGURACIÓN DEL ENTORNO DE DESARROLLO Y CODIFICACIÓN

Esta etapa consiste en transcribir o adaptar el algoritmo a un lenguaje de programación, se tendrá que adaptar todos los pasos diseñados en el algoritmo con sentencias y sintaxis propias del lenguaje.

Verificar errores, organizar el código y comentarlo, son buenas prácticas que hacen programas más legibles y facilitan la depuración.

Visita el siguiente vídeo

1.2 Planteamiento de solución de problemas según  POLYA

George Pólya fue un gran matemático que nació en Budapest en 1887 y murió en

Palo Alto California en 1985. A lo largo de su vida generó una larga lista de resultados

matemáticos y, también, trabajos dedicados a la enseñanza de esta disciplina, sobretodo

en el área de la Resolución de Problemas. Estos trabajos básicamente fueron escritos en los años cuarenta del siglo XX pero fueron traducidos hasta los años sesenta y setenta.

Se trata de un personaje clave en la Resolución de Problemas y es considerado el

pionero o gestor de las primeras etapas de esta temática.

La posición de Pólya respecto a la Resolución de Problemas se basa en una

perspectiva global y no restringida a un punto de vista matemático. Es decir, este autor plantea la Resolución de Problemas como una serie de procedimientos que, en realidad, utilizamos y aplicamos en cualquier campo de la vida diaria.

Para ser más precisos, Pólya expresa: “Mi punto de vista es que la parte más

importante de la forma de pensar que se desarrolla en matemática es la correcta actitud

de la manera de cometer y tratar los problemas, tenemos problemas en la vida diaria, en

las ciencias, en la política, tenemos problemas por doquier. La actitud correcta en la

forma de pensar puede ser ligeramente diferente de un dominio a otro pero solo

tenemos una cabeza y por lo tanto es natural que en definitiva allá sólo un método de

acometer toda clase de problemas. Mi opinión personal es que lo central en la enseñanza

de la matemática es desarrollar tácticas en la Resolución de Problemas”. 

MÉTODO DE LOS CUATRO PASOS.

Él plantea en su primer libro el llamado “El Método de los Cuatro Pasos”, para resolver cualquier tipo de problema se debe:

• comprender el problema

• concebir un plan

• ejecutar el plan y

• examinar la solución.

Para cada una de estas etapas él plantea una serie de preguntas y sugerencias.

1. Comprender el Problema.

Para esta etapa se siguen las siguientes preguntas:

• ¿Cuál es la incógnita?

• ¿Cuáles son los datos?

• ¿Cuál es la condición?

• ¿Es la condición suficiente para determinar la incógnita?

• ¿Es insuficiente?

• ¿Es redundante?

• ¿Es contradictoria?

2. Concebir un Plan.

Para Pólya en esta etapa del plan el problema debe relacionarse con problemas semejantes. También debe relacionarse con resultados útiles, y se debe determinar si se pueden usar problemas similares o sus resultados (aquí se subraya la importancia de los problemas análogos). Algunas interrogantes útiles en esta etapa son:

• ¿Se ha encontrado con un problema semejante?

• ¿Ha visto el mismo problema planteado en forma ligeramente diferente?

• ¿Conoce un problema relacionado?

• ¿Conoce algún teorema que le pueda ser útil?

• ¿Podría enunciar el problema en otra forma?

• ¿Podría plantearlo en forma diferente nuevamente? Refiérase a las definiciones.

3. Ejecución del Plan.

Durante esta etapa es primordial examinar todos los detalles y es parte importante recalcar la diferencia entre percibir que un paso es correcto y, por otro lado, demostrar que un paso es correcto. Es decir, es la diferencia que hay entre un problema por resolver y un problema por demostrar. Por esta razón, se plantean aquí los siguientes cuestionamientos:

• ¿Puede ver claramente que el paso es correcto?

• ¿Puede demostrarlo?

Él plantea que se debe hacer un uso intensivo de esta serie de preguntas en cada momento. Estas preguntas van dirigidas sobre todo a lo que él llama problema por resolver y no tanto los problemas por demostrar. Cuando se tienen problemas por demostrar, entonces, cambia un poco el sentido. Esto es así porque ya no se habla de datos sino, más bien, de hipótesis. En realidad, el trabajo de Pólya es fundamentalmente orientado hacia los problemas por resolver.

En síntesis: al ejecutar el plan de solución debe comprobarse cada uno de los pasos y verificar que estén correctos.

4. Examinar la Solución.

También denominada la etapa de la visión retrospectiva, en esta fase del proceso es muy importante detenerse a observar qué fue lo que se hizo; se necesita verificar el resultado y el razonamiento seguido De preguntarse:

• ¿Puede verificar el resultado?

• ¿Puede verificar el razonamiento?

• ¿Puede obtener el resultado en forma diferente?

• ¿Puede verlo de golpe?

• ¿Puede emplear el resultado o el método en algún otro problema?

Estas cuestiones dan una retroalimentación muy interesante para resolver otros problemas futuros: Pólya plantea que cuando se resuelve un problema (que es en sí el objetivo inmediato), también, se están creando habilidades posteriores para resolver cualquier tipo de problema. En otras palabras, cuando se hace la visión retrospectiva del problema que se resuelve, se puede utilizar tanto la solución que se encuentra como el método de solución; este último podrá convertirse en una nueva herramienta a la hora de enfrentar otro problema cualquiera.

Visita el siguiente vídeo para complementar tu información. 

1.3 Definición de algoritmo

Un algoritmo es una secuencia de pasos lógicos necesarios para llevar a cabo una tarea especifica, como la solución de un problema. Los algoritmos son independientes tanto del lenguaje de programación en que se expresan como de la computadora que los ejecuta. En cada problema el algoritmo se puede expresar en un lenguaje diferente de programación y ejecutarse en una computadora distinta; sin embargo el algoritmo será siempre el mismo.

Los algoritmos pueden ser expresados de muchas maneras, incluyendo al lenguaje natural, pseudocódigo, diagramas de flujo y lenguajes de programación entre otros. Las descripciones en lenguaje natural tienden a ser ambiguas y extensas. El usar pseudocódigo y diagramas de flujo evita muchas ambigüedades del lenguaje natural. Dichas expresiones son formas más estructuradas para representar algoritmos; no obstante, se mantienen independientes de un lenguaje de programación específico. La descripción de un algoritmo usualmente se hace en tres niveles:

Descripción de alto nivel. Se establece el problema, se selecciona un modelo matemático y se explica el algoritmo de manera verbal, posiblemente con ilustraciones y omitiendo detalles.

Descripción formal. Se usa pseudocódigo para describir la secuencia de pasos que encuentran la solución.

Implementación. Se muestra el algoritmo expresado en un lenguaje de programación específico o algún objeto capaz de llevar a cabo instrucciones.

1.4 ¿Qué es un diagrama de flujo? 

Un diagrama de flujo es un diagrama que describe un proceso, sistema o algoritmo informático. Se usan ampliamente en numerosos campos para documentar, estudiar, planificar, mejorar y comunicar procesos que suelen ser complejos en diagramas claros y fáciles de comprender. Los diagramas de flujo emplean rectángulos, óvalos, diamantes y otras numerosas figuras para definir el tipo de paso, junto con flechas conectoras que establecen el flujo y la secuencia. Pueden variar desde diagramas simples y dibujados a mano hasta diagramas exhaustivos creados por computadora que describen múltiples pasos y rutas. Si tomamos en cuenta todas las diversas figuras de los diagramas de flujo, son uno de los diagramas más comunes del mundo, usados por personas con y sin conocimiento técnico en una variedad de campos. Los diagramas de flujo a veces se denominan con nombres más especializados, como "diagrama de flujo de procesos", "mapa de procesos", "diagrama de flujo funcional", "mapa de procesos de negocios", "notación y modelado de procesos de negocio (BPMN)" o "diagrama de flujo de procesos (PFD)". Están relacionados con otros diagramas populares, como los diagramas de flujo de datos (DFD) y los diagramas de actividad de lenguaje unificado de modelado (UML).

          

Bibliografías. 

• Luis Joyanes Aguilar, Fundamentos de programación. algoritmos y estructuras de datos, Ed. Mc Graw-Hill.
• Armando E. de Giusti, Algoritmos, Datos y Programas, . Ed., Prentice Hall.

Luis Joyanes Aguilar, Fundamentos de programación. algoritmos y estructuras de datos, Ed. Mc Graw-Hill.

Mario C. Ginzburg, Introducción General a la Informática, Periféricos y Redes Locales, Biblioteca Técnica Argentina.

Armando E. de Giusti, Algoritmos, Datos y Programas, . Ed., Prentice Hall.

file:///C:/Users/Administrador/Downloads/6967-9551-1-PB.pdf 

https://www.lucidchart.com/pages/es/qu%C3%A9-es-un-diagrama-de-flujo